2015/1 -- Tarea 2

Fecha de Entrega: Viernes 14 de Mayo

Recuerden las reglas de entrega.

Para parsear una string de código fuente, como ((fun (x) (+ x 1)) 3), utilice el parser de s-expressions.

Defina un lenguaje con funciones de primera clase que contenga además variables locales con let (unario), adición y substracción, if0. Los valores del lenguajes son números y clausuras.

1. Defina el AST Expr para el lenguaje con las características mencionadas.
2. Defina la función parser :: SExpr → Expr
3. Defina la función interp :: Expr → Env → Val
4. Define la función run :: String → Val que toma un programa fuente como string, y retorna el valor después de la interpretación

Por ejemplo:

> run "((fun (x) (+ x 1)) 3)"
NumV 4

Provea tests que validen todos los casos importantes de su implementación.

Nota: Recuerde que si representa el ambiente como una lista de pares (id, val) entonces puede utilizar la función lookup provista por Haskell para buscar en el ambiente.

Extienda el lenguaje con flet (aka. fluid-let) para introducir un binding “fluido”. Un binding fluido tiene alcance dinámico. Note que dicho binding siempre tiene precedencia sobre un binding léxico del mismo identificador.

Por ejemplo:

> run "(let (x 3)
         (let (f (fun (y) (+ x y)))
           (flet (x 10)
             (f 1))))")
NumV 11

En esta parte, vamos a equipar el lenguaje de la Parte 1 con un sistema de inferencia de tipos. Esto significa que, al igual que en Haskell, vamos a checkear que un programa este bien tipado, sin requerir anotaciones de tipos en el código fuente.

El capítulo 30 del PLAI explica en detalles como funciona un inferenciador monomórfico (Si estudia desde el libro PLAI, empiece leyendo desde el 30.1.1, dado que el caso polimórfico no nos interesa en esta tarea).

Un inferenciador de tipos funciona de manera distinta a un verificador de tipos “tradicional” como los que ya vimos en clase. En particular, el sistema de tipos usa variables de tipos para denotar cada tipo desconocido y genera, al analizar un programa, una lista de constraints sobre estas variables.

Por ejemplo, si ve (fun (x) (+ x 1)), genera una nueva variable de tipo T1 para denotar el tipo desconocido de x. Luego, mirando el cuerpo de la función, genera la constraint T1=TNum para reflejar que esta es la única forma con que la función pueda estar bien tipada. El sistema de tipo produce finalmente que la expresión tiene el tipo T1→TNum con la constraint T1=TNum. Finalmente, aplicando la substitución de T1 por TNum, retorna al usuario que la expresión tiene el tipo (num→num):

> runType "(fun (x) (+ x 1))"
(num->num)

Más precisamente, el inferenciador tiene tres etapas:

1. Generar todas las constraints sin preocuparse de si son consistentes o no (es decir, sin preocuparse de si existe una solución para todas las variables de tipos tal que todas las ecuaciones sean satisfechas). Los únicos errores que se botan en esta etapa son los de identificadores libres.
2. Aplicar un algoritmo de unificación para determinar si existe una solución, y cual es. Si no hay solución, entonces es un error de tipo.
3. Si existe una solución, ésta es utilizada para reportar el tipo del programa.

Considere el siguiente tipo de dato Type:

data Type = TNum
          | TFun Type Type
          | TVar Symbol

donde TVar Symbol es una variable de tipo con un Symbol único. Cada vez que se necesite definir una nueva variable de tipo, se debe ejecutar newTVar 0 para adquirir una nueva variable de tipo con un Symbol único. Para la definición de newTVar debe considerar las siguientes librerias y definiciones:

import Data.Unique
import System.IO.Unsafe
 
type Symbol = Unique
 
newTVar _ = TVar (unsafePerformIO newUnique)

Asegúrese de definir una forma adecuada de comparar tipos (Eq) y también para imprimirlos (Show). Vea más abajo para detalles de como se espera que se impriman los tipos.

Finalmente, una constraint T1=T2 se puede representar simplemente como un par de tipos:

type Const = (Type, Type)

Estudie el capitulo 30.2 del PLAI para una explicación detallada de como generar constraints.

Defina la función typeof :: Expr -> TEnv -> (Type, [Const]) que dada una expresión Expr y un ambiente de tipos TEnv, retorna el tipo de la expresión con la lista de constraints que debe ser solucionable para que el programa sea válido en tipos. La función reporta errores solo en caso de identificadores libres; si la lista de constraints generada no es consistente, no retorna errores.

Si bien el algoritmo de unificación está descrito en el PLAI, existe una descripción más concisa y simple, proveniente de otro libro (Types and Programming Languages, B. Pierce):

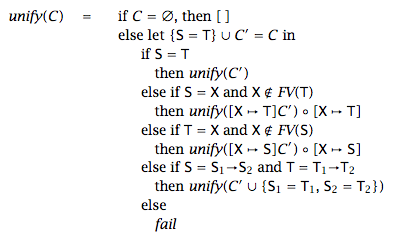
Considere que en esta definición: C es el conjunto de constraints ([Const]), S y T son metavariables que son cualquier tipo, T = X como condición expresa que T es una variable de tipo (TVar x), [X → T]C es la substitución de T por X en C, y X \notin FV(T) es para checkear que la variable X no ocurre en T (ver la discusión del occurs check en PLAI 30.5 o TAPL o wikipedia).

Defina la función unify :: [Const] -> [Const] que dada una lista de constraints retorna una lista de substitución. Una substitución es una ecuación T1=T2 donde T1 es una variable de tipo. En caso de que la lista posea inconsistencias, arroja un error.

Una vez que se obtiene la lista de substituciones de variables de tipos, el type checker debe usarla para retornar al usuario un tipo que sea lo más legible posible. Es decir, tiene que substituir todas las variables de tipos que pueda en el tipo final de la expresión checkeada.

Defina la función apply :: [Const] → Type → Type que dado una lista de substituciones y un tipo t (que típicamente contiene variables de tipos), aplica dicha substitución para obtener una versión legible del tipo.

Finalmente defina la función runType :: String → Type que dado un programa fuente como string, retorna su tipo (o arroja un error).

Ejemplos:

Se debe respetar el output exacto siguiendo el formato de los ejemplos presentados a continuación, donde runType es una función que retorna el tipo de una expresión dada como string:

> runType "(fun (x) (+ x 1))"
(num->num)
 
> runType "(fun (x) x)"
(?1->?1)
 
> runType "(fun (x) 3)"
(?1->num)
 
> runType "x"
*** Exception: free identifier x
 
> runType "((fun (x) (+ x 1)) (fun (x) x))"
*** Exception: Type error: cannot unify num with (?1->?1)