Gradual Unions: A Gradual Interpretation of Union Types
See A Gradual Interpretation of Union Types (SAS 2017)
Union types allow to capture the possibility of a term to be of several possibly unrelated types. Traditional static approaches to union types are untagged and tagged unions, which present dual advantages in their use. Inspired by recent work on using abstract interpretation to understand gradual typing, we present a novel design for union types, called gradual union types. Gradual union types combine the advantages of tagged and untagged union types, backed by dynamic checks. Seen as a gradual typing discipline, gradual union types are restricted imprecise types that denote a finite number of static types. We apply the Abstracting Gradual Typing (AGT) methodology of Garcia et al. to derive the static and dynamic semantics of a language that supports both gradual unions and the traditional, totally-unknown type. We uncover that gradual unions interact with the unknown type in a way that mandates a stratified approach to AGT, relying on a composition of two distinct abstract interpretations in order to retain optimality. Thanks to the abstract interpretation framework, the resulting language is type safe and satisfies the refined criteria for gradual languages. We also show how to compile such a language to a threesome cast calculus, and prove that the compilation preserves the semantics and properties of the language.
This tutorial covers:
- How to install the prototype implementation of GSEC+. This prototype shows interactive typing and reduction derivations for arbitrary source program.
- An overview of the application and a basic presentation of the language syntax.
- Examples of use.
An online version of this document can be found here
Installation instructions
We provide three ways to access to the the prototype implementation (although we strongly recommend the first one!):
- Using the online implementation at https://pleiad.cl/gradual-unions/.
- With the provided virtual machine, which can also be downloaded here
- Local execution of the prototype, which can be downloaded here.
The online implementation does not require any installation and is always up-to-date. If you want to get a snapshot of the current state of the interpreter (as of May 1, 2017), then follow the instructions for points 2 or 3.
The virtual machine
We have set up a virtual machine with an Ubuntu installation and Java 1.8. The virtual machine image was created with Virtual Box 4.3.28.
- Install Virtual Box 4.3.28 or higher.
- Import the Virtual Machine Image
- Start the Virtual Machine
The implementation is a play framework web server, which should start automatically on startup. Along the web server, Firefox should start automatically with the url already opened: http://localhost:9000/gradual-unions/
We also provide the steps required to start the web server manually in case it does not start automatically:
- For sudo privileges the username is “gradualunions” and the password is “1234”
- Open a terminal
- Run
service gradual-unions start
- If password is required, insert: 1234
- We also provide the restart and stop commands as well.
To change the port of the application, just edit the file /etc/init.d/gradual-unions and change the value of the variable PORT.
The application is located in
/home/gradualunions/gradual-unions-0.9/
To run the application not as a service, look at the next section (steps 4 and 5).
Local execution of the prototype implementation
To run the prototype locally, all you need is Java 1.8. Also check that you have Java 1.8 in the path.
The following instructions are Unix valid commands. If you have Windows installed in your machine, you need to perform the corresponding commands.
- Unzip the file.
unzip gradual-unions-0.9.zip
- Go to the “gradual unions ” folder:
cd gradual-unions-0.9
- Add run permissions to the binary file:
chmod +x bin/gradual-unions
- And then run:
./bin/gradual-unions
This should start a server in the port 9000. To open the application, go to http://localhost:9000/gradual-unions/
- In case the port 9000 is already taken, run:
./bin/gradual-unions -Dhttp.port=<available-port-number>
To kill the application, just press ctrl+c on the terminal running it, or kill the application (the pid of the application is located in file RUNNING_PID of the implementation folder).
Note that to run again the implentation, the RUNNING_PID file must be erased.
Overview of the prototype implementation
The following screenshot shows how the prototype implementation looks like
Given a source program, the application can shows its typing and reduction derivations.
The implementation is composed of four main areas:
The predefined examples area
Here you can select examples from a predefined list of examples. Once an example is selected, a description is shown below and the source of the example is presented in the following area.
The source program area
This is the place where you input source programs. The syntax of the language is the following:
A term can be a typed lambda abstraction, a boolean, a number, a variable, an application, an addition, a conditional or an ascription. For convenience you can write an untyped lambda (\x.t) as a shortcut for (\x:?.t).
Types can be booleans (Bool), integers (Int), unknown type (? – which may represent any type), functions and gradual union types.
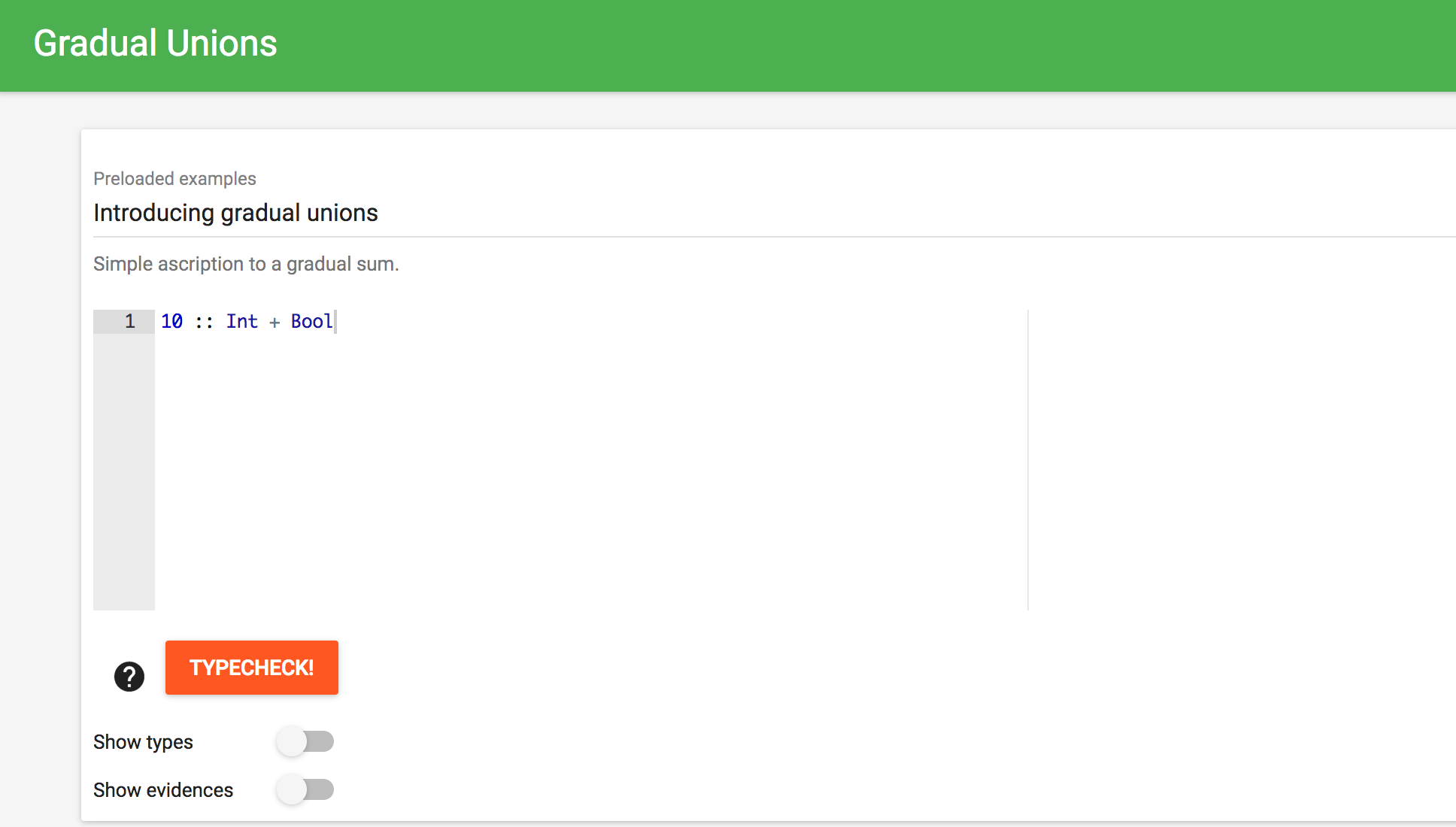
The action area
Here you can see the syntax by clicking the “?” button. Also you can type check the source program by clicking the “TYPECHECK!” button. If the source program is valid then its typing derivation is shown below, otherwise an error is shown.
The options area
Here there are two toggle buttons to show or hide types and evidences during typechecking and reduction. By default those elements are hidden.
Examples
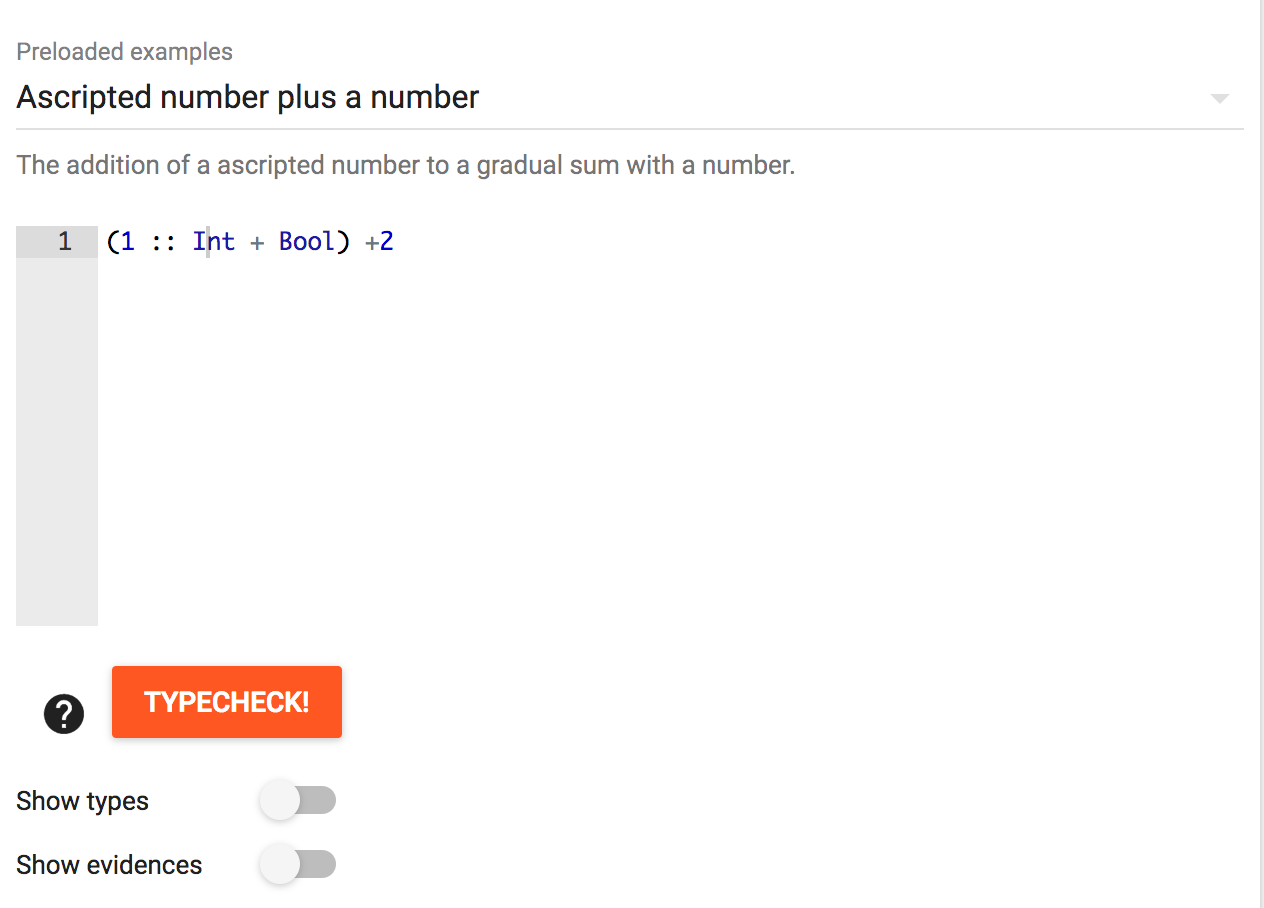
A first example
For instance let us consider the second predefined example:
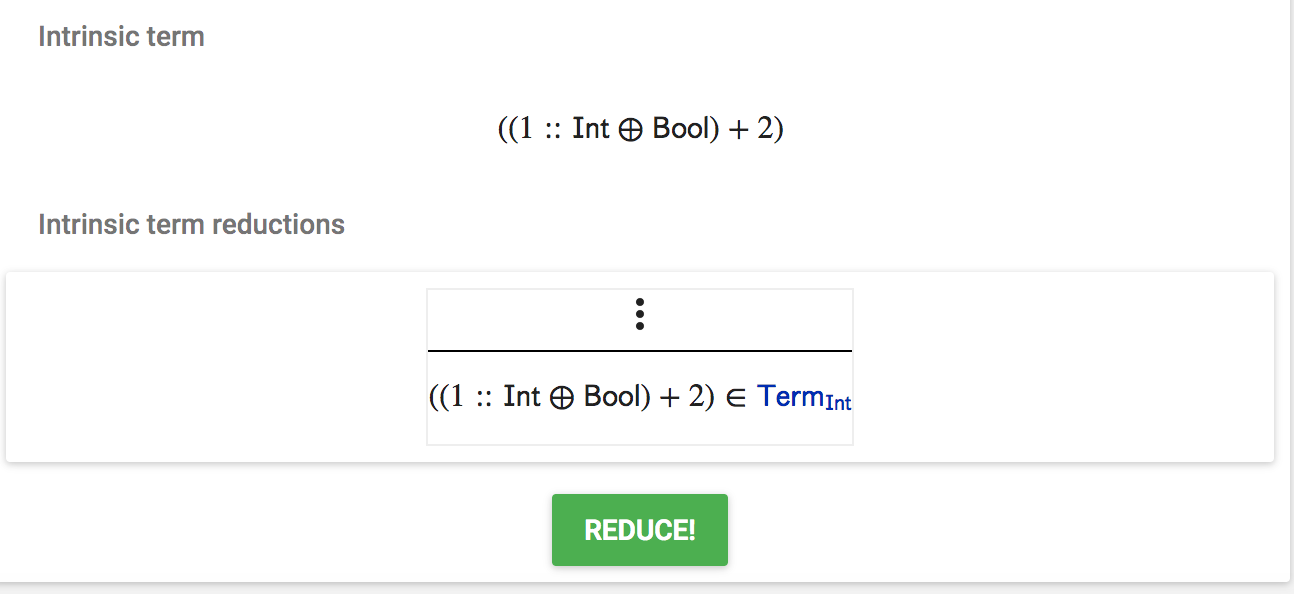
If we click the “TYPECHECK!” button, then its typing derivation is shown as follows:
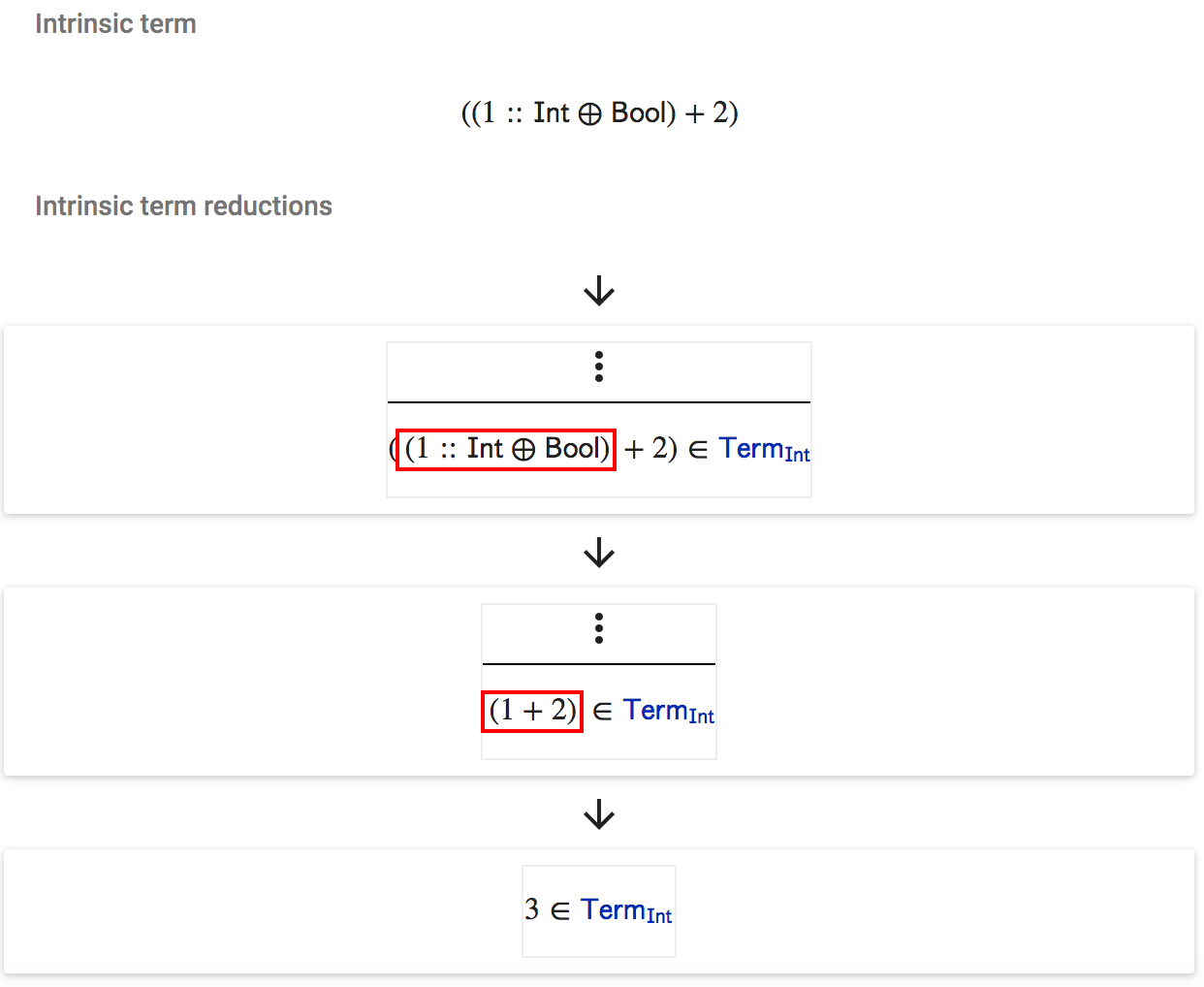
If we click the “REDUCE!” button then its reduction derivation is shown step by step as shown below:
Each step shows the redux in red.
Note as programs may loop infinitely (with ? we can encode omega), the prototype only presents the first 10 steps of reduction. If after 10 steps of reduction the program is still reducible, another button is presented to reduce another 10 steps.
The reduction of the program is presented as the reduction of intrinsic terms: derivation trees augmented with evidence. An evidence reflects the justification of why a given consistent judgment holds. Each derivation tree can be expanded by clicking the button on the top-right corner:
We can also make types explicit by activating the “show types” option:
Then the same derivation tree its shown as follows:
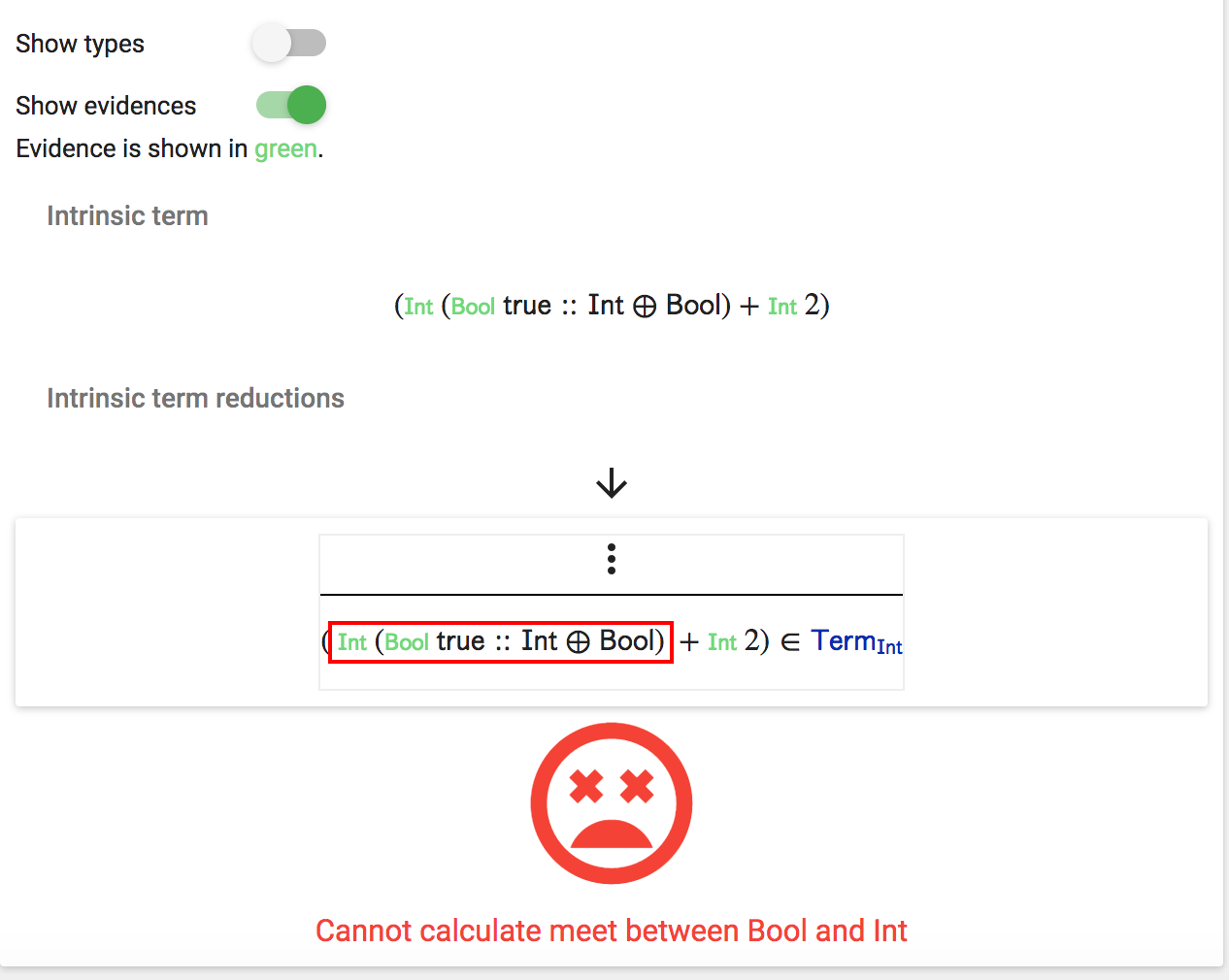
We can also show the evidences of each term in green by activating the “show evidences” option:
Then the same derivation tree is now shown as follows:
Static and dynamic errors
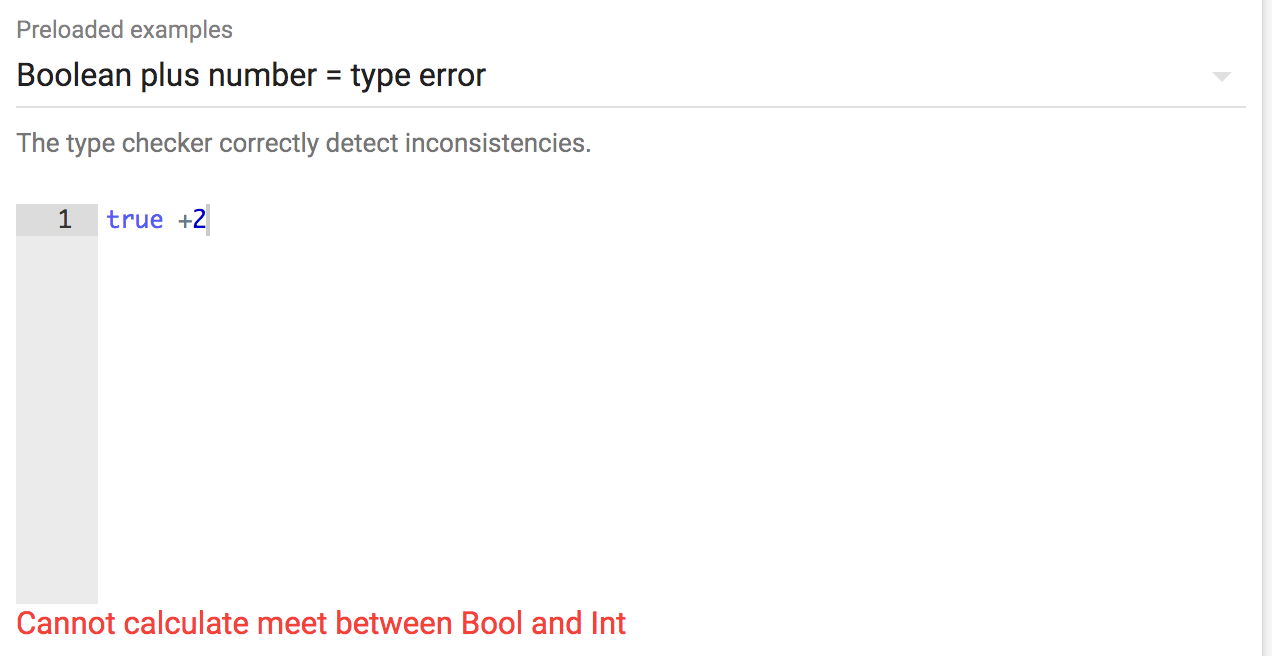
The prototype implementation reports static errors after the “TYPECHECK!” button is clicked. For example:
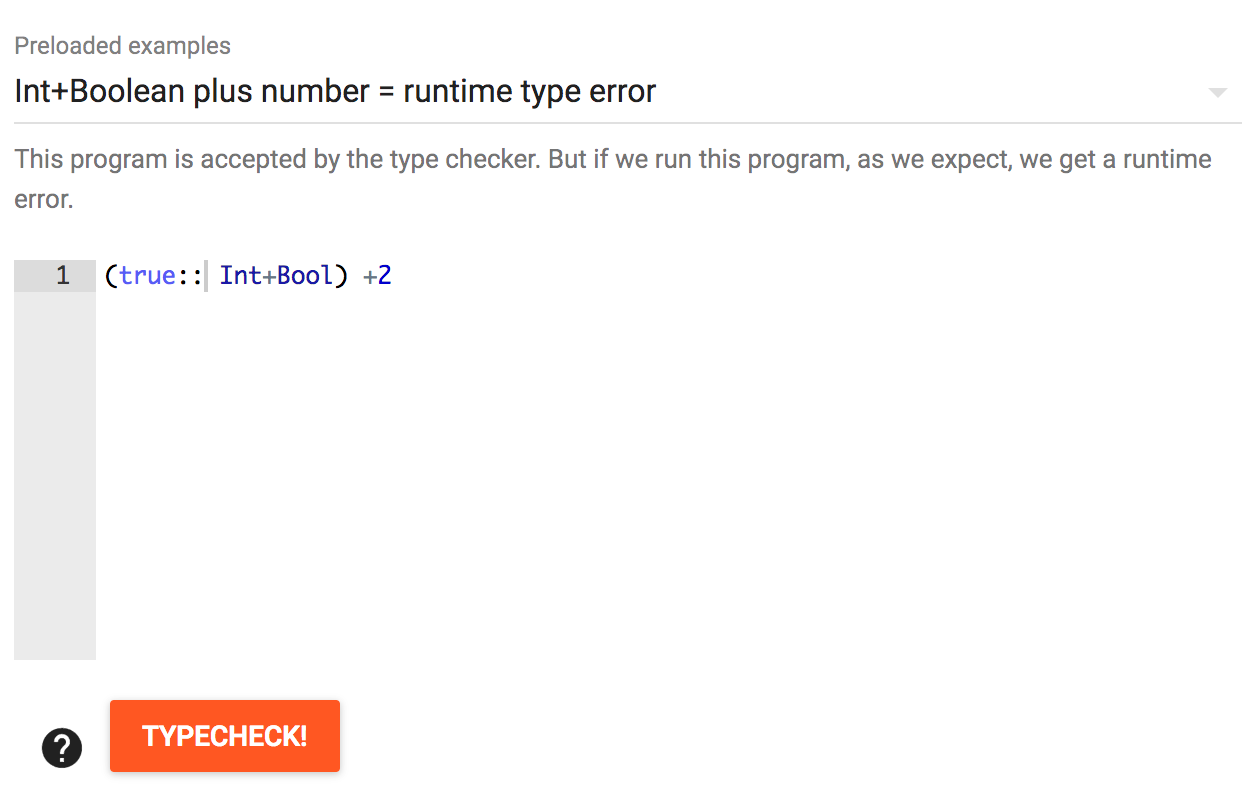
Now let us add an ascription to the boolean value:
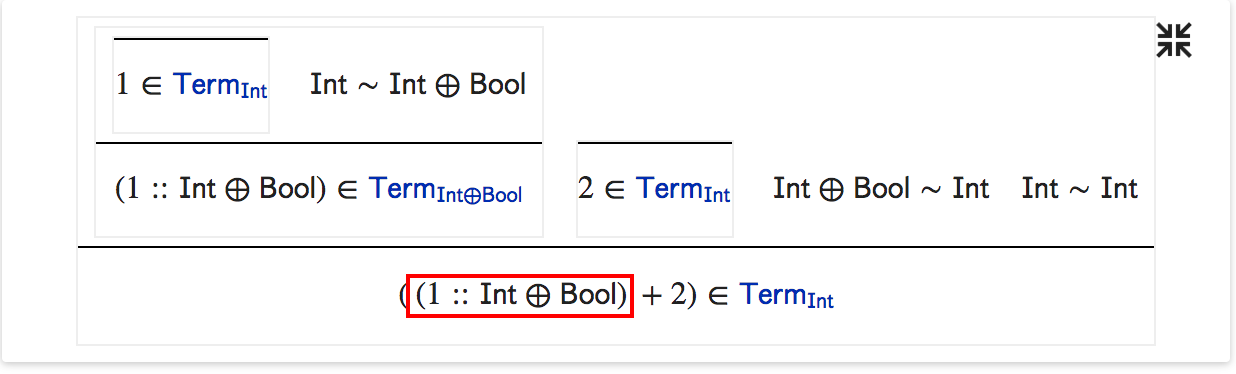
Now it is valid statically but it fails at runtime as shown below:
Combining gradual unions and the unknown type
This is an example of combining the use of gradual unions and the unknown type. The applied lambda receives either a function that receives an Int, or a function that returns an Int.
This program runs without errors as we are passing a function from Int to Int.
Now consider the following program:
This time we are passing as argument a function from Bool to Int, so the program also run without errors.
But if we consider this program:
We are now passing a function from Bool to Bool, so the program fails statically as (Int → ?) + (? → Int) is not consistent with Bool → Bool.
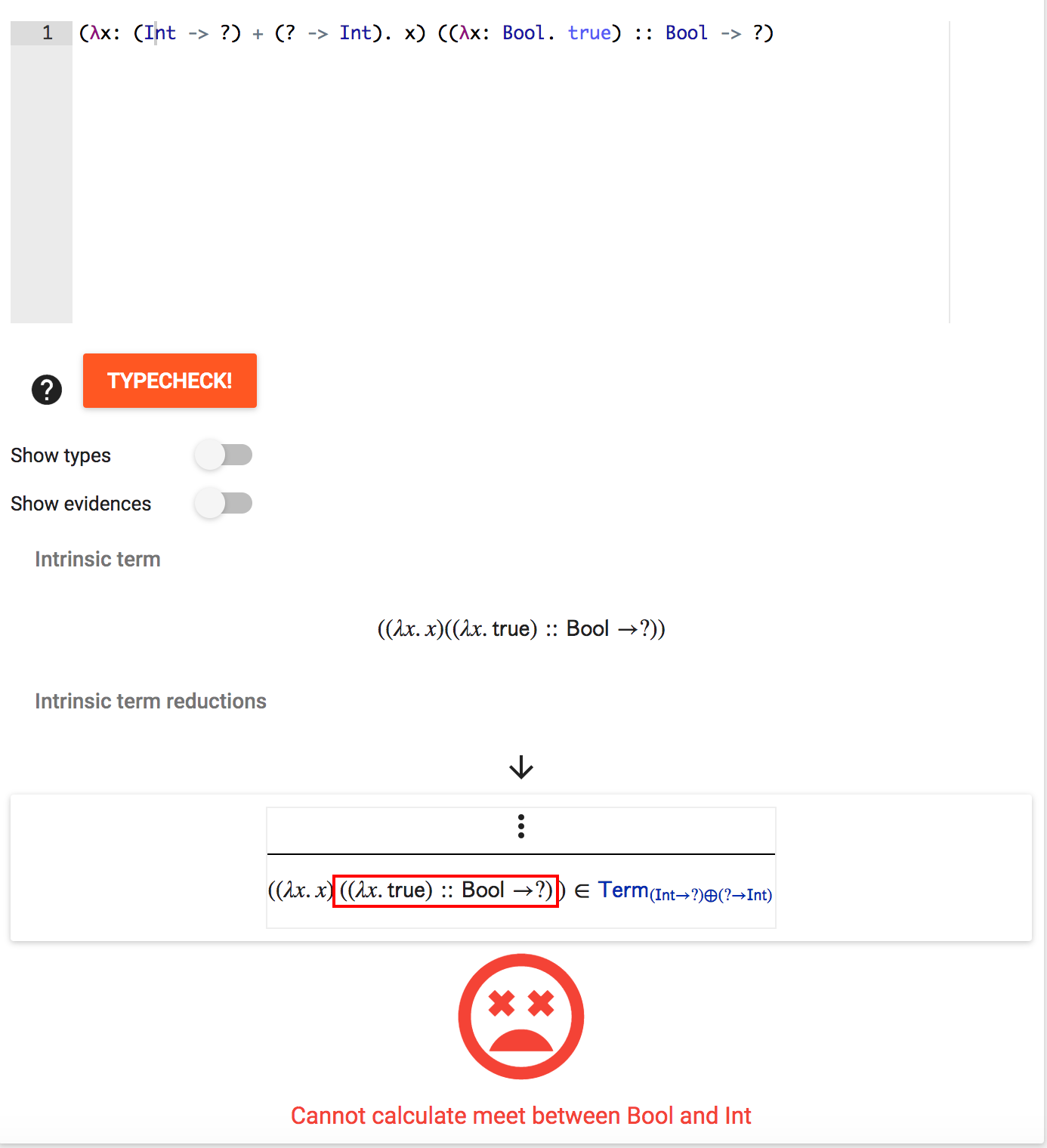
If we add an ascription to the argument:
Then the program typechecks but fails at runtime as it fails to justify that (Int → ?) + (? → Int) is consistent with Bool → Bool.