CSEC: Certified Software Engineering in Coq
The development of tools to construct software systems that respect a given specification is a major challenge of current and future research in computer science. Interactive theorem provers based on type theory, such as Coq, have shown their effectiveness to prove correctness of important pieces of software like the C compiler of the CompCert project. Certified programming with dependent types is attracting a lot of attention recently, and Coq is the de facto standard for such endeavors, with an increasing amount of users, pedagogical material, and large-scale projects. Nevertheless, significant work remains to be done to make Coq more usable from a software engineering point of view.
This collaboration project gathers the expertise of researchers from Chile (Inria Chile, Universidad de Chile, Universidad Católica de Valparaíso), France (Inria Nantes, Inria Paris) and Argentina (Universidad Nacional de Córdoba), in different areas that are crucial to develop the vision of certified software engineering. The focus of this project is both theoretical and practical, covering novel foundations and methods, design of concrete languages and tools, and validation through specific case studies.
The end result will be a number of enhancements to the Coq proof assistant (frameworks, tactic language) together with guidelines and demonstrations of their applicability in realistic scenarios.
Kick-off Workshop: March 6-9, 2018 @ DCC
Titles & abstracts of the talks
Slides of the talks are now available! Expand the abstracts to see the link.
Guillaume Munch-Maccagnoni:
Why Evaluation Order Matters The lambda-calculus in its simplest form is a very elegant base to the connections between computation, logic and algebra. However, it quickly breaks down when trying to extend it. In this introductory talk, I will present the case of sums or co-products. I will argue that it is necessary to take evaluation order into account, and show how to do it in a way that everything becomes simple again and new connections are uncovered.
Curry-Howard for RAII In a series of papers published from 1994 to 1995, Baker has promised the integration of resource management techniques from systems programming into functional programming thanks to linear logic. Many of his ideas can now be seen at the basis of the C⧺11/Rust resource management models. One of these insights is the compatibility of Stroustrup's “Resource Acquisition Is Initialisation” idiom (RAII) from old C⧺ with linearity. I will show how RAII arises naturally in the linear call-by-push-value model, an extension of intuitionistic linear logic introduced for studying the interaction of effects and resources. (joint work with Guillaume Combette)
Federico Olmedo:
Language-based Cryptographic Proofs in Coq, or Coq for Probabilistic Programs Between many others, cryptography is a field where formal, machine-aided, verification has been applied with great success. In this talk I will present CertiCrypt, a framework for building certified cryptographic proofs on top of the Coq proof assistant. The key insight behind this framework is understanding cryptographic proofs as a problem of relational, probabilistic, program verification. Throughout the talk, I will overview the different features that the framework offers for reasoning about probabilistic programs, including a complete formalization of the semantics of an imperative probabilistic language, a set of certified program transformations and a full-fledged relational Hoare logic. slides
Improving the Proof Experience in Coq As Coq users for the development of mid and large scale projects, over the years we have encountered some hurdles that usually impacted negatively in our proof development process. In these talk we will informally identify some of these obstacles and discuss related solutions that could overall improve both the user proof experience and the quality attributes of the developed proofs. slides
Pierre-Marie Pédrot:
Proof Assistants for Free Syntactic models are a particular kind of model of type theory that can be described as a program translation from some expanded type theory into a host type theory. When the latter is the Calculus of Inductive Constructions, this allows to easily create a new proof assistant for free by leveraging the Coq implementation: simply write the relatively small compiler that translates the source theory into Coq low-level terms. It is then possible to make the user believe she is living in this new theory in a relatively transparent way. slides
Weaning and The Exceptional Type Theory We describe the weaning translation, a syntactic translation of CIC that enriches it with a wide class of effects. Namely, it requires on a monadic structure that endows the type of algebras with an algebra structure itself. This translation makes explicit that the interaction of effects with dependent types is a dangerous one, as there is a notorious tension between arbitrary computation in types and dependent elimination. We present a restriction of CIC that we claim to be the generic way to allow effects and dependency to cohabitate. Nonetheless, the case of exceptions is specific as it is possible to tweak it enough to recover full dependency, at the expense of consistency. We show how to work around the latter detail and consistently enrich CIC with new principles through the resulting translation. slides
Matthieu Sozeau:
An Environment for Programming with Dependent Types, take II In this talk we present a general methodology for the development of certified, correct-by-construction programs in the Coq proof assistant. We will present the principles behind dependently-typed programming, which encompass programming with refinement types and inductive families, the links between pattern-matching compilation, the uniqueness of identity proofs principle and Homotopy Type Theory and the use of complex recursion schemes and reasoning principles on our programs. In addition, we'll also delve into the challenges of certified compilation of dependently-typed programs, bringing the high-level assurances on our programs down to their bare-metal translations. slides code
Towards Certified Meta-Programming with Typed Template Coq Template-Coq is a plugin for Coq, originally implemented by Malecha, which provides a reifier for Coq terms and global declarations, as represented in the Coq kernel, as well as a denotation command. Initially, it was developed for the purpose of writing functions on Coq’s AST in Gallina. Recently, it was used in the CertiCoq certified compiler project, as its front-end language, to derive parametricity properties, and to extract Coq terms to a CBV λ-calculus. However, the syntax lacked semantics, be it typing semantics or operational semantics, which should reflect, as formal specifications in Coq, the semantics of Coq’s type theory itself. The tool was also rather bare bones, providing only rudimentary quoting and unquoting commands. We generalize it to handle the entire Calculus of Inductive Constructions (CIC), as implemented by Coq, including the kernel’s declaration structures for definitions and inductives, and implement a monad for general manipulation of Coq’s logical environment. We demonstrate how this setup allows Coq users to define many kinds of general purpose plugins, whose correctness can be readily proved in the system itself, and that can be run efficiently after extraction. We give a few examples of implemented plugins, including a parametricity translation. We also advocate the use of Template-Coq as a foundation for higher-level tools. In the context of CSEC, we plan to use it as a basis for the formalisation of Ziliani and Sozeau's unification algorithm, and hope to be able to build on it to (i) certify tactic languages like MTac2 and (ii) execute them efficiently. (joint work with A. Anand, S. Boulier, C. Cohen and N. Tabareau) slides code
Nicolas Tabareau:
Homotopy Types and Resizing Rules: a fresh look at the impredicate sort of CIC In this talk, I will recall the basic notions of homotopy type theory and in particular the notion of homotopy n-types and of universe resizing rules, and show that it provides
a fresh look at the impredicative universe Prop of CIC. As a consequence, I will sketch a possible extension of the Coq proof assistant with definitional proof irrelevance that is currently being implemented by Gaetan Gilbert. slides
Univalent parametricity Homotopy Type Theory promises a unification of the concepts of equality and equivalence in Type Theory, through the introduction of the univalence principle. However, existing proof assistants based on type theory treat this principle as an axiom, and it is not yet entirely clear how to extend them to handle univalence internally. In this talk, we propose a construction grounded on a univalent version of parametricity to bring the benefits of univalence to the programmer and prover, that can be used on top of existing type theories. We will present a lightweight framework implemented in the Coq proof assistant that allows the user to transparently transfer definitions and theorems for a type to an equivalent one, as if they were equal.
Éric Tanter:
Foundations of Dependent Interoperability Full-spectrum dependent types promise to enable the development of correct-by-construction software. However, even certified software needs to interact with simply-typed or untyped programs, be it to perform system calls, or to use legacy libraries. Trading static guarantees for runtime checks, the dependent interoperability framework provides a mechanism by which simply-typed values can safely be coerced to dependent types and, conversely, dependently-typed programs can defensively be exported to a simply-typed application. In this work, we give a semantic account of dependent interoperability. Our presentation relies on and is guided by a pervading notion of type equivalence, whose importance has been emphasized in recent work on homotopy type theory. Specifically, we develop the notions of type-theoretic partial Galois connections as a key foundation for dependent interoperability, which accounts for the partiality of the coercions between types. We explore the applicability of both type-theoretic Galois connections and anticonnections in the setting of dependent interoperability. A partial Galois connection enforces a translation of dependent types to runtime checks that are both sound and complete with respect to the invariants encoded by dependent types. Conversely, picking an anticonnection instead lets us induce weaker, sound conditions that can amount to more efficient runtime checks. Our framework is developed in Coq; it is thus constructive and verified in the strictest sense of the terms. Using our library, users can specify domain-specific partial connections between data structures. Our library then takes care of the (sometimes, heavy) lifting that leads to interoperable programs. It thus becomes possible, as we shall illustrate, to internalize and hand-tune the extraction of dependently-typed programs to interoperable OCaml programs within Coq itself. slides
The Essence of Gradual Typing Language researchers and designers have extended a wide variety of type systems to support gradual typing, which enables languages to seamlessly combine dynamic and static checking. These efforts consistently demonstrate that designing a satisfactory gradual counterpart to a static type system is challenging, and this challenge only increases with the sophistication of the type system. Gradual type system designers need more formal tools to help them conceptualize, structure, and evaluate their designs. We present a formal foundation for gradual typing, drawing on principles from abstract interpretation, to give gradual types a semantics in terms of pre-existing static types. Abstracting Gradual Typing (AGT for short) yields a formal account of consistency—one of the cornerstones of the gradual typing approach—that subsumes existing notions of consistency, which were developed through intuition and ad hoc reasoning. Given a syntax-directed static typing judgment, the AGT approach induces a corresponding gradual typing judgment. Then the subject-reduction proof for the underlying static discipline induces a dynamic semantics for gradual programs defined over source-language typing derivations. The AGT approach does not recourse to an externally-justified cast calculus: instead, run-time checks naturally arise by deducing evidence for consistent judgments during proof-reduction. Gradual languages designed with the AGT approach satisfy, by construction, the established criteria for gradually-typed languages. We report on our experience applying AGT to various typing disciplines, highlighting the challenges of achieving type soundness (and not only type safety) when types are expected to enforce semantic properties like parametricity and noninterference. slides
Beta Ziliani:
Towards typed-tactics in Coq: the what, the why, and the how The term “tactics” is heavily overloaded, sometimes meaning small-and-simple primitives of the base theory of the prover, sometimes meaning very sophisticated meta-programs. One way or another, most tactic languages provide very loose types for tactics, making them hard to compose and maintain. In this talk I will first provide some basic understanding of tactics and tactic languages, and then present the latest achievements in a new and yet fairly unexplored view of tactics: tactics typed in the base logic of the prover. In particular, I will talk about the language Mtac2, and its application in the widely-used Iris logic framework. slides
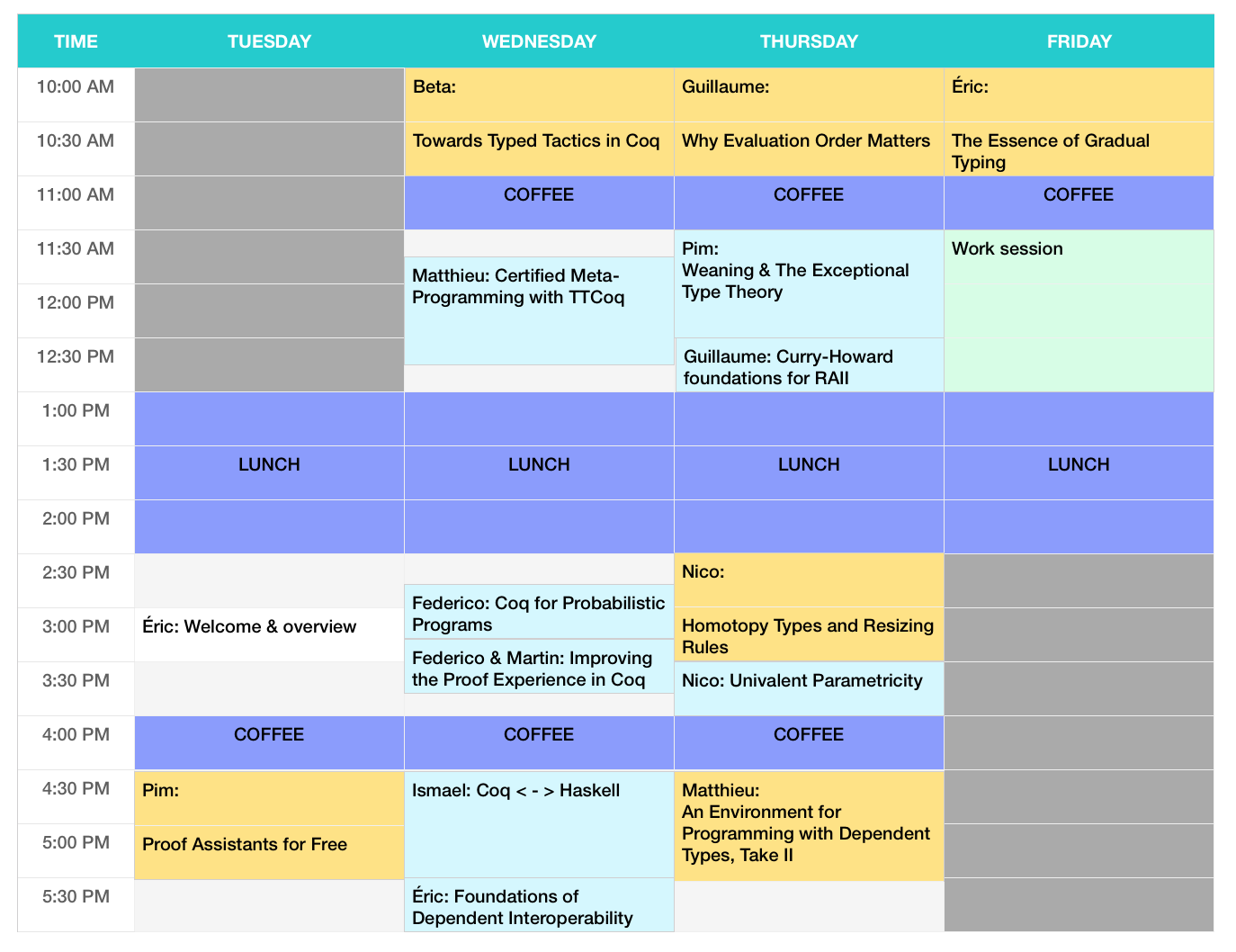
Program
Participants
Martin Bodin (U Chile)
Raimil Cruz (U Chile)
Tomas Díaz (U Chile)
Hans Fehrmann (U Chile)
Ismael Figueroa (PUC Valparaíso)
Elizabeth Labrada (U Chile)
Fabián Mosso (U Chile)
Guillaume Munch-Maccagnoni (Inria Nantes)
Federico Olmedo (U Chile)
Pierre-Marie Pédrot (MPI)
Paula Ríos (U Chile)
Matthieu Sozeau (Inria Paris)
Nicolas Tabareau (Inria Nantes)
Éric Tanter (U Chile)
Matías Toro (U Chile)
Beta Ziliani (U Córdoba)